Coeficiente de transferencia de calor total
Consideremos la situación en la que el calor se transfiere
del lado interior de un fluido, a través de un film sucio, a través de la pared
del tubo, a través de otro film de fouling al fluido exterior a una To.
Ai y Ao son respectivamente las áreas de superficie
interior o exterior para transferencia de calor para una longitud dada de
tubería. Para un tubo cilíndrico desnudo o plano:
La tasa de transferencia de calor entre el fluido en el
interior del tubo y la superficie del interior del film de suciedad viene dado
por una ecuación en la forma:
Donde el área es Ai y similarmente para el
proceso convectivo exterior donde el área es Ao. Los valores de hi
y ho tienen que ser calculados con las correlaciones apropiadas.
En la mayoría de las superficies de intercambiador de calor
real en servicio actual, se desarrollará antes o después un film o depósito de
sedimento, escala, crecimiento orgánico, etc. Algunos fluidos tales como el
aire o gas natural licuado están usualmente lo bastante limpios como para que el fouling esté ausente. La
transferencia de calor a través de estos films es preferentemente por conducción,
pero el diseñador raramente sabe lo bastante sobre espesor o conductividad
térmica del film para tratar la resistencia de transferencia de calor como un
problema de conducción. El diseñador estimará de tablas estandarizadas o a
partir de la experiencia un factor de fouling Rf. Rf se
define en términos de flujo de calor Q/A y la diferencia de temperatura a
través del fouling ∆Tf por la ecuación:
De la ecuación anterior está claro que Rf es
equivalente a un coeficiente de transferencia de calor para el fouling, hf.
y en muchos, el fouling es considerado por un “coeficiente
de transferencia de calor de fouling”, que es todavía una cantidad estimada. El
efecto de incluir esta resistencia adicional es proporcionar un intercambiador
de calor algo más grande que lo requerido cuando está limpio, así que el
intercambiador proporcionará el servicio deseado después de que haya estado
prestando servicio durante un tiempo y se haya acumulado fouling.
La tasa de flujo de calor por unidad de longitud del tubo debe ser la misma a través del film del fluido interior, el film sucio del interior, la pared, el film sucio del exterior, y el film del fluido exterior. Si requerimos que las diferencias de temperaturas a través de cada una de estas resistencias para transferencia de calor añadan diferencia de calor, (Ti – To), la obtendremos a partir de la siguiente ecuación:
En la ecuación anterior, el fouling se asume tiene un
espesor despreciable, así que los valores de ri, ro, Ai
y Ao son de tubos limpios y son independientes de la acumulación de
fouling. No solamente es conveniente.
Ahora definimos un coeficiente U* basado en cualquier área
de referencia conveniente A*
Frecuentemente, pero no siempre, A* se elige como igual a Ao,
en cuyo caso U* = Uo, y la ecuación anterior queda:
Si el área de referencia A* es elegido como Ai, el coeficiente de transferencia de calor total, viene dado por:
La resistencia de la pared es ordinariamente relativamente pequeña, y a un grado suficiente de precisión por tubos desnudos, usualmente escribimos:
La inspección de las magnitudes de los términos en el
denominador de las ecuaciones de Uo y Ui para cualquier
caso de diseño particular rápidamente revela qué términos o términos (y por lo
tanto que resistencia de transferencia de calor) predominan. Este término (o
términos) controlan el tamaño del intercambiador de calor y es en el que el
diseñador concentraría su atención. Quizás el coeficiente de transferencia de
calor puede ser significativamente mejorado por un cambio en el diseño o
condiciones de operación del intercambiador de calor. En cualquier caso, el
diseñador debe dar atención particular al cálculo o estimación del valor de la
resistencia más grande, debido a cualquier error o incertidumbre en los datos,
la correlación, o cálculo de este término tiene un efecto desproporcionadamente
grande en el intercambiador y/o fiabilidad.
Diseño integral
En los apartados anteriores, hemos obtenido una ecuación que
relaciona la tasa de transferencia de calor respecto a la diferencia de
temperatura del local (T – t) y el área de transferencia de calor A, mediante
el uso de un coeficiente de transferencia de calor A, a través del uso de un
coeficiente de transferencia de calor total U. En la mayoría de las aplicaciones
del intercambiador de calor, sin embargo, una o ambas temperaturas de la
corriente, cambian de punto a punto a través de las trayectorias del flujo de las
corrientes respectivos. El cambio en la temperatura de cada corriente se calcula
del balance de calor (entalpía) en la corriente y es un problema en
termodinámica.
La siguiente preocupación es desarrollar un método para
aplicar las ecuaciones obtenidas al caso en el que la diferencia de temperatura
entre dos corrientes no es constante.
Lo primero es escribir la ecuación del coeficiente de transferencia de calor total en forma diferencial:
Y luego formalmente integramos esta ecuación respecto a las necesidades térmicas totales del intercambiador, Qt:
U* y A* puede estar en una base consistente, pero generalmente usaremos Uo y Ao. U* puede ser, y en la práctica a veces es, una función de la cantidad de calor intercambiada. Si 1/U* (T –t) puede calcularse como una función de Q.
El procedimiento anterior puede siempre usarse, pero también es muy tedioso y consume tiempo. Podemos preguntarnos si no hay un procedimiento aceptablemente exacto que podamos usar. Haciendo ciertas asunciones, podemos integrar analíticamente la siguiente ecuación:
Donde U* es el valor (asumido constante) del coeficiente de transferencia de calor total y MTD es la “Diferencia de Temperatura Media”.
Bibliografía:
- Basic Heat Exchanger Equations. Wolverine Tube Heat Transfer Data Book.





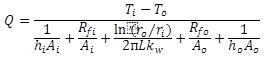







0 comentarios:
Publicar un comentario