Dedicamos
esta nuevo artículo dedicado a explicar el Control Proporcional Integral Derivativo,
una estrategia de control con muchas aplicaciones prácticas. Nos centramos
especialmente en sistemas de gestión de la energía. Los actuales sistemas de
gestión de la energía tienen una configuración jerárquica basada en un controlador
digital y también en computadores personales.
Usos y aplicaciones del control PID
La parte más
importante de un sistema de gestión de la energía son los controladores del
sistema debido a que controla la mayoría de los equipos mecánicos. Una característica
principal de los controladores de nivel del sistema son su capacidad para
manejar bucles de control múltiples y funciones tales como los controles
proporcionales-integral-derivativos (PID).
Un
controlador PID compara una señal de referencia (setpoint) respecto a una señal
actual (feedback), y con convertidores de frecuencia ajusta automáticamente la
velocidad para acoplar las dos señales. La diferencia entre las dos señales es
el valor de error (desviación). Típicamente un control PID se usa cuando la
velocidad de un ventilador o bomba necesita ser controlado basándonos en la
presión, caudal o temperatura. El control PID puede funcionar a partir de los
valores de uno o más transductores.
El control
PID proporciona una forma más exacta, precisa y eficiente para gestionar por
ejemplo sistemas de calefacción, ventilación y aire acondicionado. El software
de control adaptativo supervisa el rendimiento de un bucle particular y
automáticamente ajusta los parámetros PID para mejorar el rendimiento. Esta
característica mejora la respuesta del bucle de control y automáticamente
ajusta los parámetros PID para mejorar el rendimiento. Esta característica
mejora la respuesta del bucle de control para procesos dinámicos y complejos.
En
aplicaciones de climatización de espacios se utilizan sensores de movimiento
para determinar la ocupación. Las trampillas de las unidades terminales que
sirven al espacio se abren o cierran en función de la ecuación; y, y, las
válvulas de agua caliente o agua fría modulan bajo el control de un bucle PID
ajustable por el usuario para mantener la temperatura del espacio deseada.
Los rotores
de un motor pueden hacerse funcionar con sensores y actuadores que, a través de
un sistema de control, pueden realizar diferentes tareas, desde aliviar las
cargas desde los rodamientos a realizar un control activo del comportamiento
dinámico del sistema. El sistema de control, con sus sensores y actuadores,
puede actuar en sólo unos pocos grados de libertad del rotor, por ejemplo
suministrando amortiguación adicional, o puede controlar completamente su
posición en espacio, como ocurre en una suspensión magnética completamente
activa.
Los
rodamientos magnéticos son quizás el ejemplo más común del control activo
aplicado a las dinámicas de los rotores, pero hay muchas otras aplicaciones,
como los soportes hidrodinámicos controlados, los rodamientos electrostáticos
usados en micromáquinas, o los rodamientos neumostáticos controlados.
Los esquemas
de control PID pueden usarse con controladores PID electrónicos, hidráulicos y
neumáticos.
Es
interesante indicar que más de la mitad de los controladores industriales en
uso hoy en día utilizan esquemas de control PID o PID modificado.
Ecuaciones del movimiento en bucle abierto
Las
ecuaciones generales del movimiento de un sistema rotatorio que incluye
numerosos actuadores puede ser escrita de la siguiente forma:
Donde fc
y fn son funciones de vector forzado de tiempo del tiempo debidas,
respectivamente, a los actuadores y otras causas. La última incluye también fuerzas
desequilibradas, que son armónicos en tiempo con una amplitud proporcional a Ω2
y una frecuencia igual a Ω.
Control proporcional ideal
Un sistema
de control de realimentación proporcional suministra entradas de control que
son proporcionales a la diferencia entre las salidas actuales del sistema y y los valores de referencias r, que pueden también ser funciones del
tiempo debidas, respectivamente, a los actuadores y otras causas. La última
incluye también fuerzas desequilibradas, que son armónicos en tiempo con un
proporcional de amplitud a Ω:
Introduciendo
las ecuaciones de realimentación y salida en la ecuación de estado, se obtiene
la siguiente ecuación de bucle cerrado:
Asignando
las leyes dadas r(t) es posible introducir un control de realimentación, por
ejemplo, para compensar perturbaciones conocidas, como desequilibrios.
En caso de
un MIMO (sistema de control de salidas múltiples – entradas múltiples) las
matrices Kr y Ky tienen tantas filas como el número de
entradas de control y tantas columnas como el número de referencias y salidas,
respectivamente. Hay casos en los que el sistema de control está
descentralizado (es decir, cada entrada de control viene determinada por una
salida simple independientemente), y las señales de referencia son
suministradas para cada salida del sistema separadamente. En este caso, las
matrices Kr y Ky son cuadradas y diagonal.
El control
ideal proporcional definido arriba puede tener también acción derivativa, es
decir, introduce también amortiguación en el sistema. Como se incluyen también
velocidades generalizadas entre los estados del sistema, puede también afectar
las salidas y el control proporcional opera actualmente como un control PD
(proporcional derivativo).
Control PID
Un error en
estado estacionario puede eliminarse introduciendo un bucle de realimentación
integral, esto es un bucle de realimentación con respecto a la integral del
error de posición. Así se obtiene un regulador que a menudo se aplica a
numerosos sistemas. El regulador tiene una acción proporcional, P; integral, I;
y diferencial D.
El uso de
los valores de la ganancia proporcional y el tiempo de integración ajustan la
respuesta del sistema.
Control proporcional
El control
proporcional da como resultado una acción que es lineal con el error. El
término proporcional tiene su mayor efecto cuando el valor del proceso está
lejos del punto de ajuste deseado. Sin embargo, los valores muy grandes del
término proporcional tienden a forzar el sistema en una respuesta oscilatoria.
El efecto de la ganancia proporcional
del controlador va a cero cuando el proceso se aproxima al punto de ajuste. El
control puramente proporcional solamente se usará cuando:
·
La constante de tiempo del proceso es pequeña y
por ello puede usarse un controlador de ganancia grande.
- El cambio de carga del proceso es relativamente pequeño por lo que la compensación del estado estacionario es limitado.
- La compensación del estado estacionario está dentro de un rango aceptable.
Control integral
El control
integral produce un ajuste del proceso basado en el error acumulativo, no en su
valor actual. El término integral es el recíproco del tiempo de reset del
sistema. El tiempo de reset es la duración de cada ciclo de suma de errores. El
control integral puede cancelar cualquier compensación de estado estacionario
que ocurriría cuando se use un control puramente proporcional. Esto a veces se
llama control reset.
Un valor
bajo de la ganancia proporcional y un valor alto del tiempo de la integral
asegura una operación estable, pero proporciona una respuesta lenta.
Si el valor
de la ganancia proporcional es demasiado grande o el tiempo de la integral
demasiado corto, el sistema será inestable.
Control derivativo
El control
derivativo es un ajuste del proceso basado en la tasa de cambio de la corriente
del error de control del proceso.
El control
derivativo se usa típicamente en los casos donde hay un gran retraso temporal
entre el dispositivo controlado y el sensor usado en la realimentación. Este
término tiene el efecto total de prevenir que la señal del actuador vaya muy
lejos en una dirección u otra, y puede usarse para excederse en la limitación.
Controlador PID en dominio tiempo
El
controlador PID puede representarse en una variedad de modos. En el dominio
tiempo, la salida del controlador viene dada por:
Controlador PID en el dominio s
Es
relativamente directo derivar la transformación de Laplace de la ecuación PID
del dominio tiempo. La función de transferencia del controlador es:
Esta función
de transferencia del controlador puede ser multiplicado por la función de
transferencia del proceso para producir la función de transferencia adelante
total G de un modelo de proceso de dominio s. El criterio descrito
anteriormente puede ser usado para valorar la estabilidad de todo el sistema.
Ver 2ª PARTE



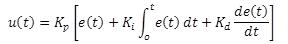

3 comentarios:
¿Por qué los controladores integral y/o derivativo no pueden trabajar sin el proporcional o solos?
Y el proporcional si puede trabajar solo
Muy buena introducción ya entendí gracias les recomiendo
Publicar un comentario