a. Computación básica
La
resolución de problemas de fluidos implica la aplicación de una o más de las
tres ecuaciones básicas: continuidad, momento y energía. Las tres herramientas
básicas se desarrollaron a partir de la ley de conservación de masa, la segunda
ley del movimiento de Newton y la primera ley de la termodinámica.
Para una
densidad variable la ecuación puede ser escrita:
Donde
- A es la sección transversal de la tubería.
- V es la velocidad media en la misma localización.
- Q es el caudal.
- ρ es la densidad del fluido.
- m caudal másico
La ecuación
es válida para cualquier conducto rígido
en toda su longitud si no hay adiciones o pérdidas de líquidos entre
secciones.
Para un
caudal de tubería en estado estacionario, la ecuación del momento relaciona la
fuerza neta en una dirección dada (Fs) actuando en un volumen de control (una
sección del fluido en el interior de la tubería), el flujo de momento neto a
través del volumen de control.
Para flujo
incomprensible esta ecuación puede reducirse a:
Estas
ecuaciones pueden fácilmente ser aplicadas a problemas de flujo
tridimensionales añadiendo ecuaciones en las direcciones y y z.
Una forma
general de la ecuación de la energía aplicable a una tubería o conducto
incomprensible es:
Las unidades
son energía por peso unitario de líquido:
Que se
reduce a ft o m. El primero de los tres términos es la altura de presión
Altura de
elevación (Z)
Y altura de
velocidad
Los últimos
tres términos del lado de la ecuación son la altura dinámica añadida por una
bomba (Hp) o quitado por una turbina (Ht) y la fricción más pérdidas de altura menor (Hf). La suma de los tres
primeros términos de la ecuación se definen como la altura total, y la suma de
las alturas de elevación y presión se refieren como la altura piezométrica.
El propósito
de este análisis es determinar los cambios de presión resultantes en los
fluidos incomprensibles en sistemas de tuberías. Ya que las tuberías de
secciones circulares son comunes en aplicaciones de ingeniería, nos centraremos
en la geometría circular. Sin embargo, los resultados pueden generalizarse para
una tubería de geometría no circular sustituyendo para el diámetro D en
cualquiera de las ecuaciones, el diámetro hidráulico, Dh, definido
como:
El análisis
que realizamos puede también aplicarse a gases y vapores, probado que el número
Mach en el conducto no excede de 0,3. Para valores mayores del número Mach, el
efecto de comprensibilidad puede ser significativo.
b. Fricción del fluido
El cálculo
de la pérdida por fricción en tuberías y conductos depende de si el flujo es
laminar o turbulento. El número de Reynolds es el ratio de fuerzas de inercia
respecto a fuerzas viscosas y es un parámetro conveniente para predecir si en condiciones
de flujo será laminar o turbulento. Esto se define como:
- V es la velocidad de flujo media.
- D el diámetro.
- Densidad del fluido = ρ
- Peso específico = Υ
- Viscosidad = ѵ
- Velocidad del flujo = V
Puede
realizarse un análisis dimensional para proporcionar una relación funcional
entre la pérdida de fricción Hf, dimensiones de tuberías,
propiedades de fluidos, y parámetros del caudal. La ecuación resultante se
llama ecuación de Darcy – Weisbach:
El factor de
fricción f es una medida de la rugosidad de la tubería. Se ha evaluado
experimentalmente para numerosas tuberías. Los datos se usan para crear el
factor de fricción de Moody, Para Re < 2000, el caudal en una tubería será
laminar y f es sólo una función de ReD. Esto puede calcularse por:
Con los
números de Reynolds entre 2000 y 4000 el flujo es inestable como resultado del
comienzo de la turbulencia. En este rango, los cálculos de pérdida de fricción
son difíciles debido a que es imposible determinar un valor único de f. Para Re
> 4000 el caudal es turbulento y f es una función de Re y rugosidad de la
tubería relativa (e/d). En Re altos,
f eventualmente depende solo de la rugosidad de la tubería. El flujo luminar en
las tuberías es inusual. Por ejemplo, para el agua fluyendo en una tubería de
diámetro 0,3 m, la velocidad tendría que estar por debajo de 0,02 m/s para
flujo laminar. Por lo tanto, la mayoría de los problemas de flujos están en la
región turbulenta.
Mediante un
Moody chart obtendremos f requerido para que Re y r/d sean conocidos. El
cálculo de Re es directo si la temperatura del agua, velocidad, y diámetro de
la tubería son conocidos. El problema es obtener un buen valor de e.
Ya que la
rugosidad puede variar con el tiempo debido a la acumulación de depósitos
sólidos o crecimientos orgánicos, f es también dependiente del tiempo. Las
tolerancias de fabricación también causan variaciones en el diámetro de la
tubería y rugosidad de superficie. Debido a estos factores, el factor de
fracción de cualquier tubería puede sólo ser aproximado.
Wood
desarrolló ecuaciones que pueden ser usadas en lugar del diagrama de Moody para
estimar f para Re > 104 y 10-5 < k < 0,04 (k = e/d).
El problema práctico
es todavía obtener un valor fiable para e. No puede medirse directamente pero debe ser
determinado a partir de ensayos de fricción en la tubería.
Una solución
exacta usando la ecuación Darcy-Wisbach puede requerir una solución de prueba y
error debido a la dependencia de f en
Re si el caudal o el diámetro de la tubería no se conocen. Una aproximación
típica para solventar este problema es estimar una velocidad del fluido
razonable para calcular Re y obtener f de la ecuación de Moody. Seguidamente, calculamos
una nueva velocidad y repetimos hasta que la solución converge.
Ver 2ª PARTE












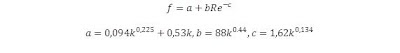
0 comentarios:
Publicar un comentario